Coincidence or destiny?

[Goldstein]

Hi -

While collecting Russian and Baltic silver for over 40years sometimes very strange coincidences happen.
Here some examples:
2 napkin rings from Lorie, bough in different years in different countries (belonging probably to two sisters Tanja and Valeria)






Big surprise - 5 years later I found this spoon in England






Sugarstrainer from Riga - within 3 years








Cigarette case by Khlebnikov - within 10 years






It is a pity that the objects can not tell what twisted ways they took from Russia/Riga to me.....

Regards
Goldstein

[Aguest]

Computers will increase the chance of this happening, I found a silverware set with a Scottish family monogram and then I used the search engines and found a communion cup in the same pattern by the same maker with the same Scottish family monogram, so I had located 2 generations :::

If the hobby has become an obsession and thousands of days are spent in the pursuit silver objects, then I vote for destiny over coincidence, even though the chances of this happening are so low it is almost impossible :::

[Qrt.S]

Mind my saying but my Russian tells me that the name on the first picture's napkin ring is ГАЛИНА, in Latin letters Galina. Tanja is spelled ТАНЯ

[Goldstein]

Hi -

you are right - it is Galina n o t Tanja!

Thanks for correcting.

Regards
Goldstein

[Joerg]

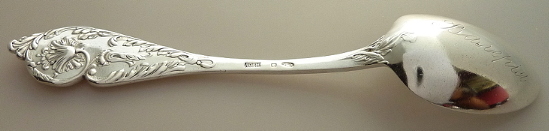
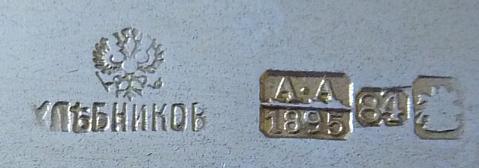Hi Goldstein
this is a nice variation of the "Birthday Problem".
https://en.wikipedia.org/wiki/Birthday_problem
The birthday problem deals with the number of people required so two people share the same birthday. We tend to overestimate this number because there are 365 days in a year. In reality, for a 50% probability of a matching birthday, a sample of 23 people are required, while if you go for a 90% probability, you need 41 people. You can check this in your nursery home: If you find 30+ inmates who still remember their birthday, there is a very high probability for a match.
The solution is, you are looking for ANY match. There are much higher sample required, if you search for a specific match. So you will probably have difficulties to find in your nursery home an inmate with the same birthday as you have.
Moving on to Russian silver: You were not looking for a match for a specific item in your collection, but for any match within your vast collection. We can look at two problems:
First: How high is the probability that Goldstein got two matching items in his collection bought at different times and places?
Second: If Goldstein’s matches of two items are within the normal probability range, how many pieces in total are out there?
The math behind this problem is complicated, but manageable. We need some assumptions:
For the first one, we need to guess how many Imperial Russian items are out there available to be collected. The value may be large, but is limited. And how many of them are matching items.
I do not know if I calculated correctly, but if there are 5 million pieces out there, in a collection of 5000 items you have a 90% probability for a match, and the chances are very high for two or more matches. Now, this is a wild calculation, but with some time and further analysis, we can conclude we most probably do not have coincidence or destiny here but rational probabilities.
Have fun, I was assuming you have 5000 items by the fact you collect for 40 years and you seem to have an intake of at least 10 items a month….
Regards, Jörg

[Goldstein]

Hi Joerg -

thank you for your effort - but the "Birthday Problem" does not work if you look for persons with red hairs!
The same with my silver: you need to find the identic maker also.....next to the pattern!
I wanted to start a little experiment in my nursery home - not easy - some are dement - others are twins - most have not red hairs.
Now I am uneasy - why do I have only a few matching objects when it is only a rational probability and I should have two or more matches?
What did I wrong?

All the best
Goldstein